Converting Odds into Probabilities… and Vice Versa

If you can’t convert odds into the probabilities they imply, you are going to struggle in the long term to make money from your betting. How can you assess value if you don’t first know the probabilities the betting market is indicating?

It’s not a difficult thing to do and with a little practice you will be able to do it automatically every time you look at a betting market.

First we’ll look at conversion of fractional odds to probabilities as those are still the predominant type used in the UK.

 

Converting Fractional Odds

Fractional odds simply reflect  the return you will get if your selection wins – bet £20 on a 4/1 shot and you’ll get £80 - 4 x £20 – back (plus your original stake of £20). However, they also reflect the bookmaker’s assessment of the chances of that selection winning . In addition, there's an adjustment in there to cover the bookmaker’s profit margin (the overround) but for the purposes of this exercise we’ll ignore that.

So what percentage chance does the bookmaker think a selection has if he is offering 4/1?  Here’s the calculation:

Divide the number on the right of the fraction by the total of both numbers in the fraction:

1 divided by (4+1) = 0.20

Then multiply that by 100 to give a percentage probability:

0.20 x 100 = 20%

So a 4/1 chance has an implied 20% chance of winning! Simples

 

Converting Decimal Odds

Again, like fractional, decimal odds are a reflection of the return you will receive if you win, including your stake. So if you have £20 on a winner with decimal odds of 7.0, you will receive £20 x 7 for a return, including stake, of £140 (£120 profit). To convert those odds into a probability, here’s the calculation:

Divide 1 by the decimal odds then multiply by 100 to give a percentage

1 divided by 7 = 0.143

0.143 x 100 = 14.3%

So a selection priced at 7.0 in decimal format has an implied 14.3% chance of winning!

 

These are very simple calculations and with experience you will be able to look at a betting market and instantly calculate the implied winning chance of all the runners based on the odds on offer.

Vice Versa

If you have reached the point where you are compiling your own tissue prices as part of a value finding exercise (and that should be your aim!), you will need to be able to convert percentage probabilities back to odds format for the purpose of comparison.

 

Converting Probabilities to Fractional Odds

 

Based on your own assessment methods, you have determined that a horse has a 10% chance of winning a race. To convert that into fractional odds format the calculation is

(100 divided by percentage probability) -1

(100/10) -1

10-1 = 9

So a selection with a 10% chance of winning should be priced at 9/1

 

Converting Probabilities to Decimal Odds

 

In this example you’ve found a horse that you think has a 60% chance of winning it’s race. To calculate it’s odds in a decimal format:

Divide 100 by the percentage probability

100/60 = 1.66

So a 60% chance is expressed as 1.66 in decimal odds format.

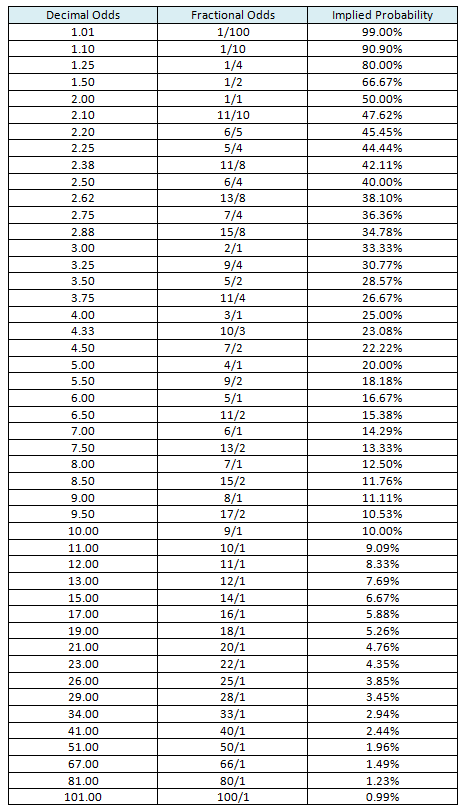
So there you have it. However, an even easier way to do it is to memorise the major odds and their respective implied probabilities using the table I have put together below!